반도체의 전기적 특성에 영향을 끼치는 중요한 요소는 소스단자/채널에서 형성되는 캐리어 농도와 분포입니다. 이를 파악할 때 페르미-디락 분포확률함수(Fermi-분포확률함수)를 활용하면 편리합니다. 페르미-디락 분포확률함수의 값은 일반적으로 ‘에너지 상태가 전자에 의해 점유될 확률’을 의미합니다. 이를 쉽게 표현하면 ‘어떠한 에너지 상태일 때, 전자가 최외각궤도에 존재할 확률’로 풀이할 수 있습니다(여기서 에너지란 페르미-디락 분포확률함수의 독립변수로써 운동에너지와 정전기적 위치에너지를 포함한 개념입니다). 이번 장에서는 페르미-디락 분포확률함수를 통해 온도변수와 농도변수, 반도체 type 변수에 따른 캐리어의 존재 확률에 대해 알아보도록 하겠습니다.
최외각전자의 원자 내 존재확률 @T=0[K], 진성 실리콘 반도체
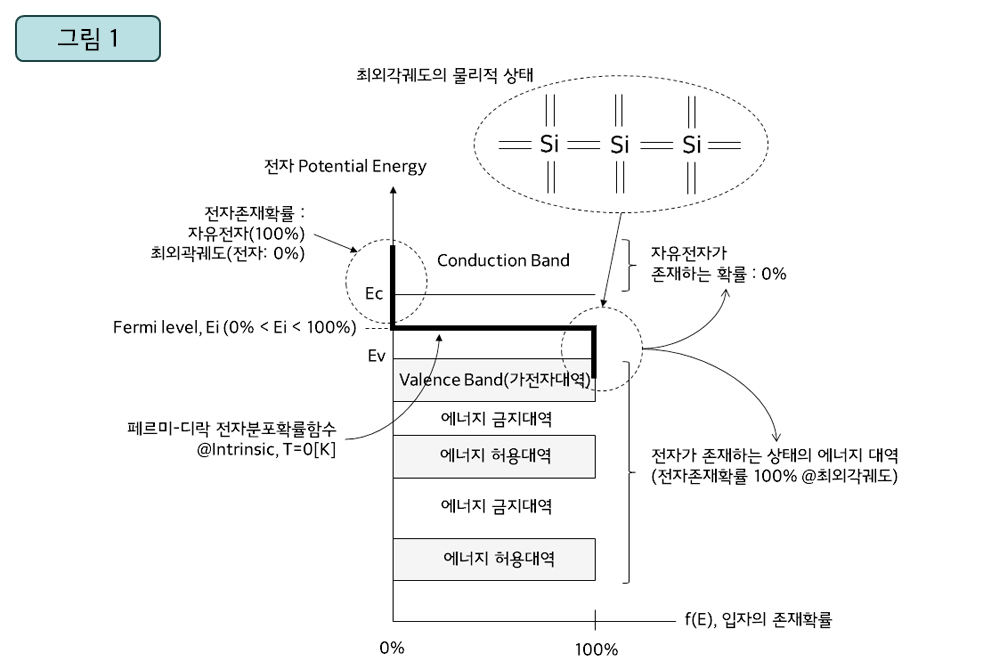
▲ 진성반도체의 에너지 밴드와 페르미-디락 전자분포확률함수 @T=0[K]
절대온도 T=0[K]의 전제조건
절대온도 T=0[K]인 섭씨 -273도에서는 전자의 이동이나 불순물의 이온화가 불가능합니다. 따라서 극저온에서는 전자가 에너지를 흡수하여 전도대로 여기)하거나 원자 내 천이(전자가 에너지를 방출하여 원자 내 낮은 궤도로 이동)하는 현상 등이 발생하지 않지요. 그럼에도 불구하고 동결현상이 발생하지 않는다는 가정 하에 페르미-디락 분포의 확률함수를 해석함으로써, 극저온과 상온의 온도 구간에 걸쳐 나타나는 전자들의 분포상태와 움직임을 알아보고자 합니다.
전자들이 에너지를 흡수하면 최외각궤도를 탈출(여기: Exitation)하게 됩니다. <그림1>의 페르미-디락 전자분포확률함수에서 전자의 포텐셜(Potential) 에너지(y축, 독립변수)가 Ev인 경우, 페르미-디락 전자분포확률함수의 종속변수(x축 값)인 전자들이 100% 확률로 최외각궤도에 존재하게 되어 모든 전자들이 원자 내 머물게 됩니다.
그러다가 전자의 포텐셜 에너지가 Ev에서 Ei(진성실리콘의 페르미 에너지 Level) 미만까지 증가하면 최외각전자들의 운동이 약간 활발해집니다. 그럼에도 불구하고 에너지가 불충분하여 전자가 최외각궤도에서 탈출할 확률은 제로(공유결합에 참여한 상태 그대로)이지요. 그런데 포텐셜 에너지가 Ei로 증가한 경우, 페르미-디락 분포에 따르면 최외각궤도에서 전자가 탈출하기 시작하여 최외각궤도에 0%에서 100%까지 존재할 확률(이 경우 몇 %의 확률인지 알 수 없는 상태이나 평균 50%임)을 유지하게 됩니다. 그 후 최외각전자들의 포텐셜 에너지가 Ei보다 높아지면 최외각궤도에서 전자가 모두 탈출하여 원자 내 전자의 존재 확률이 제로가 되지요(그러나 실질적으로는 원자핵과 전자 사이에 정전기력이 작용하는 구심력 측면으로 볼 때 전자가 하나씩 최외각궤도에서 탈출할 때마다 구심력이 기하급수적으로 상승하므로, 전자의 100% 여기 같은 형상은 발생되지 않음. 심지어 상온에서도 이런 경우는 발생되지 않음).
정공의 원자 내 존재확률 @T=0[K], 진성 실리콘

▲ 진성반도체의 에너지 밴드와 페르미-디락 정공분포확률함수 @T=0[K]
정공인 경우 이웃 원자에서 전자가 여기(탈출)하는 매커니즘은 동일하지만, 전자인 경우와 반대로 해석됩니다. 먼저 정공의 포텐셜 에너지는 전자인 경우와 반대 방향입니다. 정공의 실체는 전자의 빈 자리이므로, 언제나 원자라는 바운드리 안에 묶여 있습니다. 그러므로 에너지 대역도 가전자 에너지대(가전자대역)까지만 존재할 수 있으며, 원자 밖 에너지 준위인 전도대역 의 에너지 대에서는 정공의 존재 자체가 의미가 없지요.
조건 또한 절대온도 T=0[K] 등을 비롯해 전자인 경우와 동일한 상태로 설정합니다. 정공의 포텐셜 에너지(독립변수)가 <그림2>의 y축에 따라 변할 때, 페르미-디락 정공분포확률함수에 따라 정공이 최외각궤도에 존재할 확률값f(E)을 x축 상에서 구합니다. 에너지가 Ev인 경우 최외각전자들이 최외각궤도에 가득 차있으므로 최외각궤도에서 정공의 존재확률은 0%가 됩니다. 포텐셜 에너지가 Ei인 경우에는 전자가 최외각궤도에서 100%~0%의 확률로 유지되므로, 최외각궤도에서 정공의 존재확률은 0%~100%가 됩니다(전자인 경우와 마찬가지로 정공인 경우도 몇 %의 확률인지 알 수 없는 상태이나 평균 50%임). 최외각전자들의 포텐셜 에너지가 Ei보다 높아질 경우(정공의 포텐셜 에너지가 감소)는 최외각궤도 내 전자의 존재 확률이 제로가 되므로 정공이 존재할 확률은 100%가 됩니다(즉 실리콘의 최외각껍질에는 전자가 하나도 없는 상태, 즉 모두 정공만 있는 셈이지만, <그림1>의 설명과 동일한 이유로 실질적으로는 이와 같은 경우는 발생되지 않게 됨).
최외각전자의 원자 내 존재확률 @T=0[K], 외인성 실리콘


▲ 외인성반도체의 에너지 밴드와 페르미-디락 전자분포확률함수 @ T=0[K]
MOSFET의 소스단자(+드레인단자)를 형성하기 위해 5족 불순물 양이온을 빔이온으로 집결시켜 스캐닝 방식으로 진성실리콘인 웨이퍼에 주입합니다. 먼저 웨이퍼에 산화막이나 LPCVD/HDP CVD, 혹은 ALD로 막을 형성한 후, 포토>식각>에칭>세정공정을 거쳐 절연막 위에 포토마스크의 패턴을 형성시킵니다. 연이어 이온주입과 어닐링(RTA)공정을 진행해 트랜지스터의 소스와 드레인 단자를 동시에 (포토마스크의 패턴이 절연막을 거쳐 웨이퍼 표면 밑으로 이동) 준비합니다.
nMOSFET인 경우 실질적으로는 P-type Substrate에 농도가 약 100~1,000배 이상 높은 반대 type인 5족 불순물(N-type)로 도핑하여 소스/드레인 단자를 형성시킵니다. 실리콘 원자 개수가 1x10^22개/cm^3인 진성실리콘반도체(실질적으로는 P-type 반도체로써, 3족 원자가 1x10^15~16개/cm^3)에 5족-불순물도핑(약 1x10^18개/cm^3)을 하면, 페르미-디락 전자분포확률함수 전체의 포텐셜 에너지는 도핑 농도에 비례하여 상승하지요(진성실리콘일 때와 비교하여). 따라서 Ec와 페르미-디락 전자분포확률함수 사이의 에너지 간격이 줄어들기 때문에(진성실리콘과 비교해 볼 때, 외인성 실리콘은 페르미 레벨도 Ei에서 Ef로 상승함) 보다 적은 Latent 에너지를 투입해도 4족-5족의 공유결합된 전자(잉여전자 포함)가 공유결합력과 원자핵이 당기는 구심력을 끊어내고 원자로부터 탈출할 수 있답니다. 외인성 실리콘에서 포텐셜 에너지 변화에 따라 최외각궤도 상에 존재하는 전자의 확률(<그림3>)은 진성실리콘에 대한 페르미-디락 전자분포확률함수의 결과(<그림1>)와 유사합니다.
정공의 원자 내 존재확률 @T=0[K], 외인성 실리콘


▲ 외인성반도체의 에너지 밴드와 페르미-디락 정공분포확률함수 @ T=0[K]
pMOSFET인 경우 소스단자(+드레인 단자)를 형성하기 위해 3족 불순물을 도핑합니다. 그 결과 페르미-디락 정공분포확률함수 전체의 포텐셜 에너지는 정공 에너지가 증가하는 방향으로 도핑 농도에 비례하여 상승합니다(진성실리콘과 비교했을 때 외인성 실리콘은 페르미 레벨도 동일하게 Ei에서 정공의 Ef로 상승함). 따라서 Ev와 페르미-디락 정공분포확률함수와의 에너지 간격이 줄어들어 보다 적은 Latent 에너지를 투입해도 인접의 공유결합하고 있던 전자들이 정공으로 이동하여 채우게 되고, 이동 전 전자들이 있던 자리에 새로운 정공을 만들게 됩니다. 외인성 실리콘에서 포텐셜 에너지 변화에 따라 최외각궤도 상에 존재하는 정공의 확률(<그림4>)은 진성실리콘에 대한 페르미-디락 정공분포확률함수의 결과(<그림2>)와 유사합니다.
최외각전자의 원자 내 존재확률 @T=300[K], 진성 실리콘
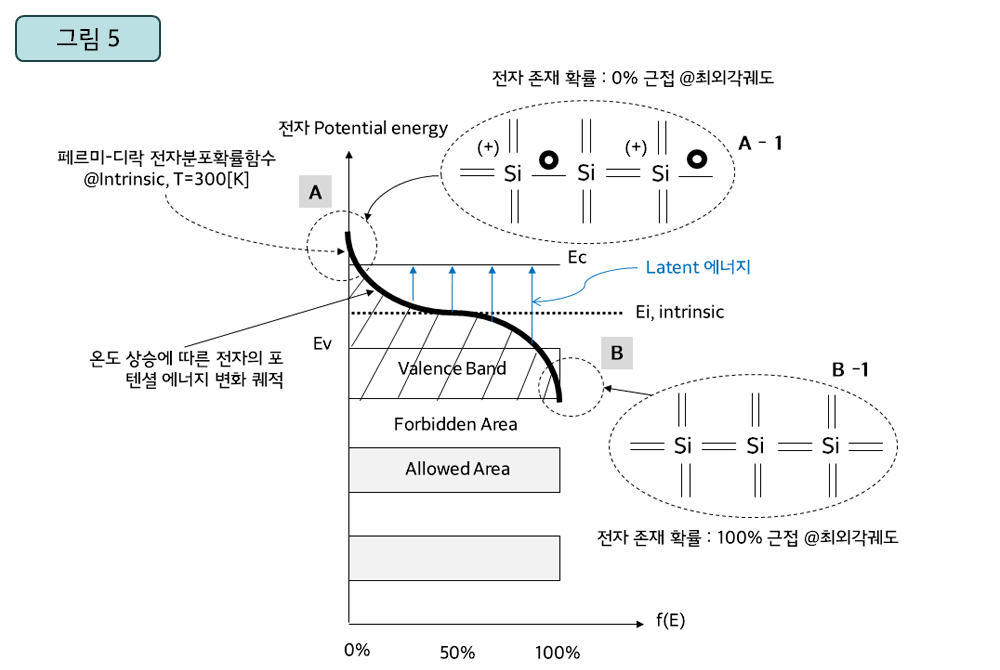
▲ 진성반도체의 에너지 밴드와 페르미-디락 전자분포확률함수 @ T=300[K]
진성실리콘인 경우, 온도가 절대온도 T=0[K]에서 상온(T=300[K])으로 상승하면 페르미-디락 분포확률함수그래프의 기울기가 확률50%를 중점으로 가파르게 상승 합니다(그래프 기울기는 온도에 비례). 온도의 상승이 전자가 보유하고 있는 포텐셜 에너지를 높여주면서 그만큼 반비례하여 Latent에너지를 줄여주지요.
물리적으로 볼 때, 온도 상승에 따라 공유결합을 하고 있던 전자들의 운동이 더욱 활발해져서 보다 많은 수의 전자들이 최외각궤도를 이탈하여 자유전자가 됩니다. 그리고 최외각궤도에는 전자가 빠져나간 숫자에 비례하여 정공의 숫자가 늘어나지요(<그림5>의 A와 B부분은 페르미-디락분포 보다는 볼츠만이 간략화 시킨 볼츠만-근사 분포로 표현할 수 있지만, 볼츠만-근사 분포도 큰 범위로는 페르미-디락 분포 범주에 포함됨). A-1과 B-1은 전자가 y축의 포텐셜 에너지(독립변수)를 보유할 때, 최외각궤도 상에서 전자가 존재할 확률(x축 종속변수의 값)과 물리적인 결합 현황을 나타낸 것입니다. Ec와 페르미-디락 전자분포확률함수가 나타내는 y축 값의 차이는 Latent 에너지로써, 이는 일정한 포텐셜 에너지를 보유하고 있는 전자가 여기하는 데 소요되는 에너지입니다.
정공의 원자 내 존재확률 @T=300[K], 진성 실리콘
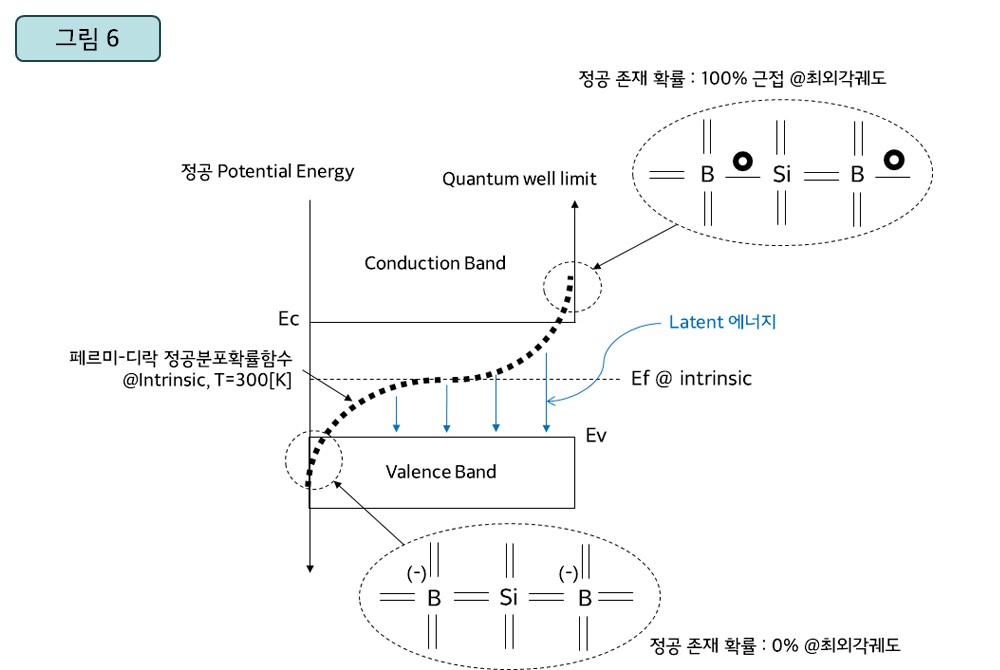
▲ 진성반도체의 에너지 밴드와 페르미-디락 정공분포확률함수 @ T=300[K]
상온/진성실리콘이라는 조건 아래 정공의 원자 내 존재 확률과 최외곽궤도상의 물리적 상태 등을 알아볼 때에는, <그림5>의 전자 관점을 <그림6>의 정공 입장으로 바꿔 이해하면 됩니다. 단, 정공의 포텐셜 에너지 방향은 전자와 반대 방향이므로, 에너지와 관련된 정공은 전자의 경우와 반대로 해석해야 합니다. 정공의 이동 메커니즘은 전자와는 판이하게 다른데, 정공에 대한 흐름은 전자의 징검다리 이동으로 해석합니다.
최외각전자의 원자 내 존재확률 @T=300[K], 외인성 실리콘

▲ 외인성반도체의 에너지 밴드와 페르미-디락 전자분포확률함수 @ T=300[K]
외인성(Extrinsic) 실리콘인 경우, 5족 불순물의 도핑(소스/드레인 단자) 농도에 비례하여 페르미-디락 전자분포함수의 궤적이 (전자에너지가 높아지는 방향으로) 상승합니다. 그에 따라 진성실리콘에 비해 전자가 원자로부터 적은 에너지(Latent 에너지)로도 탈출 가능하게 됩니다. 즉, 최외각궤도에 있는 전자들의 포텐셜 에너지가 높아져 보다 많은 수의 전자들이 원자로부터 탈출(전도대로 여기)할 수 있게 되는 것이지요. <그림7>의 A와 B부분은 원자 내 최외각궤도 상에 존재하는 전자들의 물리적 상태를 보여줍니다. A는 낮은 포텐셜 에너지(거의 Ev 수준)를 보유한 전자는 대부분 원자 내에 머물러 있는 상태를(이 경우, Latent 에너지가 거의 밴드갭인 Eg 수준임), B는 높은 에너지를 보유한 대부분의 전자들이 여기된 이후의 4족-5족의 결합상태를 보여주지요. 보통 이온 주입 농도는 Si14 원자대비 1천분의 1개에서 1만분의 1개(5족 원소) 정도 입니다.
결국 온도와 도핑 농도가 상승하면, 전자들의 포텐셜 에너지가 높아지고, 전기적으로 마이너스를 띄는 잉여전자 개체수도 많아져 원자핵으로부터의 구심력(정전기적 위치에너지)이 약해지므로(페르미-디락 전자분포 함수의 궤적이 상승하는 효과로 Latent 에너지가 줄어듦) 원자에서 탈출하여 자유전자가 되는 전자의 개체 수(또한 확률적으로도 전자 자체적인 개체수가 많아짐)가 증가하지요. 그에 따라 nMOSFET의 소스단자에서 드레인 단자로 흐르는 전류량이 증가하는 효과가 발생합니다.
정공의 원자 내 존재확률 @T=300[K], 외인성 실리콘
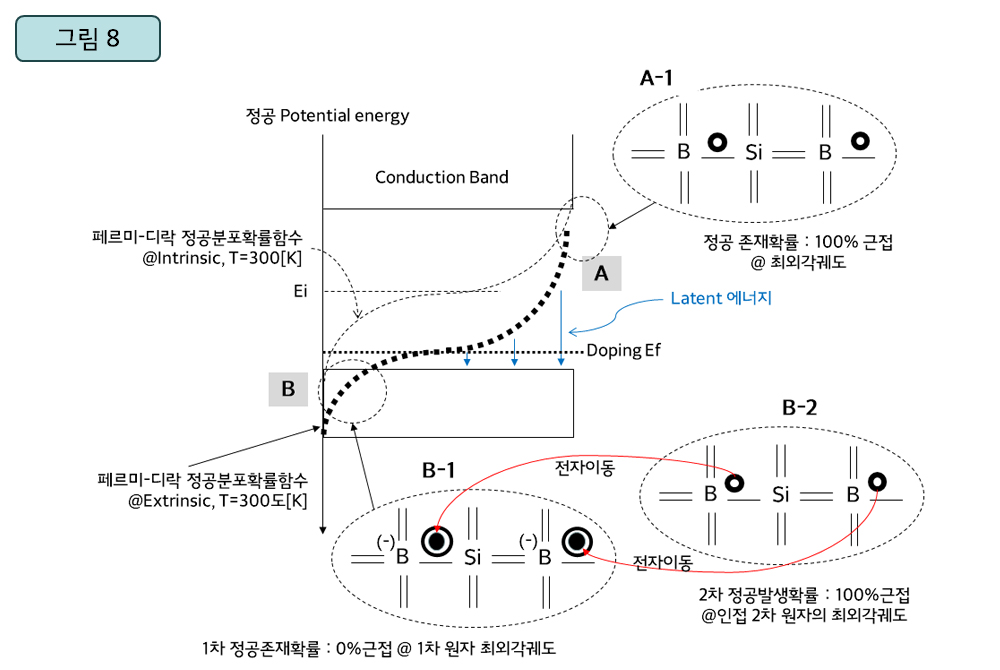
▲ 외인성반도체의 에너지 밴드와 페르미-디락 정공분포확률함수 @ T=300[K]
외인성(Extrinsic)실리콘인 경우, 3족 불순물의 도핑(소스/드레인 단자) 농도에 비례하여 페르미-디락 정공분포함수의 궤적이 (정공에너지가 높아지는 방향으로) 상승합니다. 그에 따라 진성실리콘에 비해 적은 에너지(Latent 에너지)로도 정공이 원자 내에서 쉽게 발생하게 됩니다. 실질적으로는 도핑으로 3족 불순물 숫자가 많아져 인접해 있는 전자들이 3족-4족 결합이 만들어 놓은 정공 속으로 들어갈 가능성이 확률적으로 높아진 것이지요. 3족-4족 결합에 의한 정공 개체 수에 비례하여 이웃 전자를 끌어당기는 전기적 인력이 높아져 전자들이 쉽게 정공 속으로 끌려들어가게 되고, 전자들이 떠난 자리에 또 다른 정공(2차적으로 발생)을 만들어 놓습니다. 이런 일련의 인력들이 작용하여 페르미-디락 정공분포함수의 포텐셜 에너지를 높이고(궤적을 정공에너지가 높아지는 방향으로 상향시키고) Latent 에너지를 적게 만듭니다. <그림8>의 A-1와 B-1,-2는 원자내 최외각궤도 상에 존재하는 정공들의 물리적 상태를 나타내주지요. A-1은 낮은 포텐셜 에너지(A:거의 Ec 수준)를 보유한 정공이 대부분 원자내에 머물러 있는 상태이고요(이 경우, Latent 에너지가 거의 밴드갭인 Eg 수준임). B-1은 높은 에너지(B)를 보유한 대부분의 정공들이 인접 원자의 최외각전자를 끌어와 채운 후의 물리적 상태를 보여줍니다. 끌려 온 전자가 끌려오기 전 위치에 다른 정공을 발생시킨 물리적 상태가 B-2이지요.
결국 온도와 도핑 농도가 상승하면, 정공(실체적으로는 전자)들의 포텐셜 에너지가 높아지고, 전기적으로 플러스를 띄는 정공들의 개체수도 많아져서 이웃 원자의 전자를 끌어당기는 인력(정전기적 위치에너지)이 강해집니다(페르미-디락 정공분포 함수의 궤적이 상승하는 효과로 Latent 에너지가 줄어 듦). 이는 pMOSFET의 소스단자에서 드레인 단자로 흐르는 전류량을 증가시키는 효과로 이어지게 됩니다.
원자 내 분포된 캐리어(전자와 정공)들이 온도변수와, 농도변수 및 반도체 type 변수에 따라 어떤 확률로 존재하는지를 페르미-디락 캐리어분포확률함수를 통해 해석해보았습니다. 본 장에서는 특히 에너지적인 요소와 환경변화가 실질적으로 원자, 특히 최외각전자에 어떤 영향을 끼치는지를 전자와 정공의 물리적 상태로 나타내고자 했습니다. 이와 함께 나중에 소개될 전자들이 존재 할 수 있는 상태를 나타내는 상태밀도(DOS)를 결합하면 반도체의 각 단자 혹은 Layer에서 캐리어들이 실질적으로 얼마나 존재하는지를 에너지적으로 산출할 수 있고, 이를 이용하여 캐리어의 개수(농도)와 분포 상태 및 전도도를 추정할 수 있겠습니다.
'정리하는 반도체 > 반도체 공학' 카테고리의 다른 글
| 다수 캐리어와 소수캐리어 (0) | 2020.06.02 |
|---|---|
| 상태밀도함수 (0) | 2020.06.01 |
| 반도체에서 자유전자 (0) | 2020.05.29 |
| 반도체 전자와 에너지 (0) | 2020.05.28 |
| 메모리 반도체 전압 인가 방식 - Word line & Bit line (0) | 2020.05.26 |



