드레인 전류는 캐리어(Carrier, 전자 혹은 정공)의 농도에 의해 좌우되기도 하는데, 캐리어 농도는 주로 캐리어의 확률적 개체수와 상태밀도에 의해 정해집니다. 미시세계에서의 캐리어는 전자와 정공이고, 캐리어의 확률적 개체수는 캐리어 알갱이들의 숫자와 위치에 따라 판단하는데요(이는 지난 챕터에서 다룬 페르미-디락분포확률함수로 추정할 수 있습니다). 이러한 캐리어들은 원자(단독원자 혹은 다원자)의 결합구조 속에 위치해있습니다. 이번 장에서는 단위공간과 단위에너지 안에서, 미시세계 내 캐리어들의 상태의 수를 나타내는 상태밀도(Density Of State, DOS)에 대해 알아보겠습니다.
원자의 결합구조는 에너지의 산물
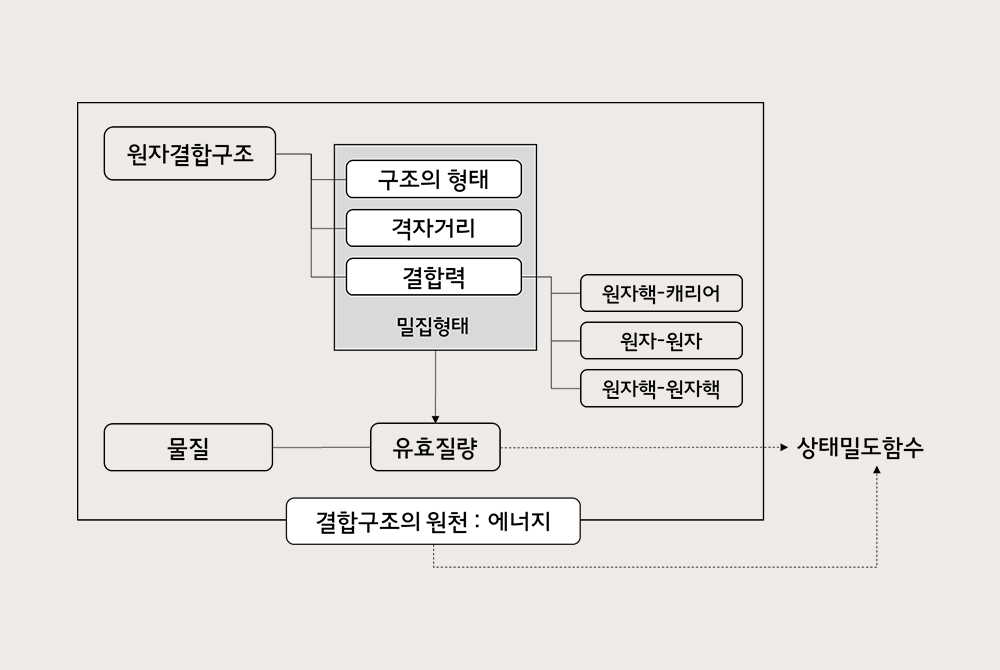
▲ 원자결합구조의 원천, 에너지
고체를 형성하는 수많은 원자는 서로 결합하여 격자구조를 형성하며, 이는 일정한 형태로 반복되어 있습니다. 이러한 격자구조는 형태, 격자 간격, 내•외부에서 가해지는 인력 등에 의해 영향을 받는데요. 결정격자구조는 저절로 형성되는 게 아닌, ‘에너지’가 원천이 되어 에너지의 변화(높고 낮음)에 따라 형태나 간격, 결합력 등이 결정됩니다.
또한 격자구조의 변화(격자구조 혹은 형태, 원자핵과 원자간 거리, 서로 영향을 끼치는 결정 내 내부 힘의 변수 등)에 따라 캐리어의 겉보기 질량도 달라집니다. 이렇듯 격자구조 내 여러 가지 변수에 따라 영향을 받아 나타나는 질량을 ‘유효질량’이라 합니다. 이 유효질량은 상태밀도함수에 영향을 끼치게 됩니다.
상태와 상태밀도

▲ 캐리어의 상태밀도
‘상태’란 여러 가지 의미를 내포하지만, 여기서는 협의의 의미로 결합구조(결정격자의 형태, 격자간 거리, 격자 내에서 내외부적으로 작용하는 상호인력을 포함)를 의미합니다. ‘상태밀도’는 그러한 결합구조들이 단위 체적 혹은 단위 에너지당 얼마나 밀집되어 있는지를 알아내는 지표이지요. 상태밀도가 높다는 것은, 구조밀도가 높아 캐리어(전자나 정공)들이 존재할 수 있는 상태가 많이 만들어져 있다는 것을 의미입니다.
캐리어들이 존재해야 하는 상태의 입장에서 볼 때, 원자의 안과 밖의 상태는 서로 다릅니다. 전자의 존재는 주로 원자 밖(원자와 원자 사이)에서 다루고(에너지 영역으로는 도전(Conduction Band) 영역), 정공은 주로 원자 내에서 다루지요(에너지 영역으로는 최외각전자(Valence Band) 영역). 왜냐하면 전류에 기여하는 전자는 원자 밖에 있는 경우이고, 정공은 원자 내에 있는 경우이기 때문입니다(전자가 원자 내에 기여하는 경우는 전자가 원자와 원자 사이를 이동하는 경우인데, 이는 곧 정공의 이동이라고 봄).
따라서 상태밀도를 의미하는 DOS는 캐리어가 원자의 결정격자구조 내에 존재하는 상태의 미시적 개념으로써, 단위 체적 및 단위 에너지(양자화 에너지) 영역 내 양자역학적 입자들의 에너지 상태의 수를 의미합니다.
페르미-디락 캐리어분포확률함수 vs 상태밀도함수

▲ 에너지 변수에 따른 전자와 정공의 상태밀도함수 D(E)
페르미-디락 캐리어분포확률함수와 상태밀도함수의 입력(함수의 독립변수)은 모두 에너지를 변수로 합니다. 이는 에너지 이외에 미시세계에서 나타낼 수 있는 적정한 인자(입력값 혹은 독립변수)가 없을 뿐 아니라, 에너지 변수가 원자의 안과 밖의 상황을 그나마 가장 정확하게 대변해줄 수 있기 때문입니다.
출력(함수의 종속변수)을 보면, 페르미-디락 캐리어분포확률함수는 캐리어들이 얼마나 많이 존재하고 있는지를 확률값으로 나타냅니다. 또 상태밀도함수는 캐리어들이 존재할 자리인 상태들에 대한 밀도 값을 제시해줍니다. 전자(혹은 정공)에 대한 상태밀도는 Ec 이상(정공은 Ev 이하)의 에너지를 입력(독립변수로)하면 각 캐리어들이 존재할 상태에 대한 결과를 Conduction Band(정공은 Valence Band) 영역에서 함수값으로 출력합니다.
농도와 캐리어 개체수
캐리어는 N타입과 P타입에서 각각 2개(다수캐리어/소수캐리어)씩, 총 4가지 형태로 나타나는 전자와 전공을 의미합니다. 요지는 미시세계 기준에서의 캐리어 개체수를 계산해야 한다는 데 있습니다. 거시적 세계에서는 일반적으로 밀도에 전체 면적 혹은 전체 체적을 곱하여 알갱이 수를 셉니다. 예를 들어 서울시청 앞에 모여있는 사람들의 수를 세는 경우, 평방미터당 몇 명이 존재하는지(밀도)를 알면, 사전에 계산된 전체 면적에 밀도를 곱하여 총인원 수를 간단히 알 수 있지요. 체적의 경우도 동일한 방식입니다.
그런데 미시세계에서는 단위 체적당 알갱이 수를 셀 수 없으므로 대신 농도를 구합니다. 농도는 거시적 개념의 밀도에 비해 오차범위가 커질 수 있지만, 현재 적용할 수 있는 Index는 농도보다 적합한 게 마땅히 없지요. 따라서 캐리어 수는 농도에 해당 체적을 곱하여 구하고, 체적은 단위 체적을 목적하는 공간까지 적분하여 계산합니다.
캐리어 농도

▲ 캐리어 농도에 영향을 끼치는 요소들
캐리어의 농도는 페르미-디락분포확률함수 x 상태밀도함수로 구할 수 있습니다. 즉 캐리어 농도를 높이려면, 첫째로 이온임플란테이션의 이온의 도즈(Dose)를 높이고 이온주입에너지를 조절하여 단위 체적당 주입된 캐리어의 숫자를 증가시켜야 합니다. 둘째로는 상태밀도를 높여야 합니다. 상태밀도를 높인다는 것은 원자결합의 변수(격자구조, 형태, 거리, 인력 등)를 조절하여 캐리어가 존재할 수 있는 최적의 상태를 얼마나 밀도 있게 형성하느냐입니다. 단, 여기에는 에너지가 존재하는 영역만 해당합니다(Forbidden Area에 대해서는 고려해야 할 것이 많지만 Forbidden Area Eg는 해당되지 않음).
유효농도

▲ 전자와 정공의 개체수 산출 @ Intrinsic 반도체 <출처: “NAND Flash 메모리”>
유효농도는 실질적인 캐리어의 개체수에 영향을 끼치는 농도를 말합니다. 유효농도의 값은 같은 전자, 같은 정공이라도 반도체의 타입(N타입/P타입)에 따라, 혹은 에너지 밴드에 따라 다르게 나타납니다. 즉, 유효농도는 일률적인 절대농도가 아니라 상황과 변수에 따라 상대적으로 적용되는 농도이지요.
유효농도는 먼저 캐리어 타입이 결정된 후, 캐리어가 존재할 Site가 확보되어야 하고, 확보된 Site 내 캐리어가 존재해야 합니다. 여기서 존재할 Site란 거시적인 개념이고, 미시적 개념은 Conduction Band 혹은 Valence Band가 결정된 후의 캐리어의 상태이며 이는 유효질량 변수가 포함된 상태밀도함수(DOS의 함수)로 구합니다. 캐리어가 존재한다는 것은 미시적으로는 확인이 불가능하므로 존재의 확률을 구해 유추해야 하는데요. 이 확률은 외부변수에 따라 변하므로, 이를 확률함수로 구현한 것이 페르미-디락 분포확률함수입니다. 확률함수의 독립변수는 측정 및 컨트롤이 가능한 변수로 에너지를 사용했습니다. 독립변수(에너지)를 확률함수에 입력하면 존재의 확률이 얼마나 되는지 용이하게 계산되지요. 캐리어의 상태밀도함수의 독립변수도 컨트롤 가능한 변수여야 하고, 캐리어에 직접적인 영향을 끼치는 Index여야 하므로 분포의 확률함수와 마찬가지로 에너지가 적당합니다. 따라서 위에서 구한 상태밀도를 확률함수로 곱하면 캐리어가 존재하는 유효농도(Effective Concentration)가 계산됩니다.
상태밀도함수에 에너지를 입력변수로 대입하면, 해당되는 에너지 레벨(Energy Level)에 대한 상태밀도가 구해집니다. 이를 구하는 궁극적인 목적은, 상태밀도함수와 페르미-디락 분포확률함수를 결합하여 조건 및 범위가 주어졌을 때 캐리어의 개체수를 확률적으로 계산하기 위함이지요. 캐리어 개체수를 알아내면 회로에 흐르는 전류를 추정할 수 있습니다. 설계된 전류의 최솟값을 달성하기 위해 단자와 기판(Substrate)에 어느 정도의 농도로 도핑을 하고, 정션(Junction)에는 전압을 얼마나 인가할 것인가를 결정합니다. 그래서 드레인에 전류를 얼마나 흘려 MOSFET을 동작시킬 것인지에 대한 입력 조건들과, 그로 인한 동작 결과를 비교함으로써 반도체를 더 깊이 이해할 수 있습니다.
'정리하는 반도체 > 반도체 공학' 카테고리의 다른 글
| DRAM 작동원리! (0) | 2020.06.08 |
|---|---|
| 다수 캐리어와 소수캐리어 (0) | 2020.06.02 |
| 페르미-디락 분포확률함수와 전자의 존재 확률 (0) | 2020.05.30 |
| 반도체에서 자유전자 (0) | 2020.05.29 |
| 반도체 전자와 에너지 (0) | 2020.05.28 |


